Model Fuzzy Sugeno dan Tsukamoto Beserta Studi Kasusnya

 Model Fuzzy Sugeno dan Tsukamoto Beserta Studi Kasusnya

        Logika fuzzy merupakan salah satu pembentuk soft computing. Logika fuzzy pertama kali diperkenalkan oleh Prof. Lotfi A. Zadeh pada tahun 1965. Dasar logika fuzzy adalah teori himpunan fuzzy. Pada teori himpunan fuzzy, peranan derajat keanggotaan sebagai penentu keberadaan elemen dalam suatu himpunan sangatlah penting. Nilai keanggotaan atau derajat keanggotaan atau membership function menjadi ciri utama dari penalaran dengan logika fuzzy tersebut. (Kusumadewi & Purnomo, 2010) Ada beberapa definisi logika fuzzy, diantaranya :

1. Logika fuzzy adalah logika yang digunakan untuk menjelaskan keambiguan, logika himpunan yang menyelesaikan keambiguan. (Vrusias, 2008).
2. Logika fuzzy menyediakan suatu cara untuk merubah pernyataan linguistik menjadi suatu numerik. (Synaptic, 2006).

        Logika fuzzy memiliki derajat keanggotaan dalam rentang 0 hingga 1. Berbeda dengan logika digital yang hanya memiliki dua nilai 1 atau 0. Logika fuzzy digunakan untuk menerjemahkan suatu besaran yang diekspresikan menggunakan bahasa (linguistic), misalkan besaran kecepatan laju kendaraan yang diekspresikan dengan pelan, agak cepat, cepat, dan sangat cepat. Dan logika fuzzy menunjukan sejauh mana suatu nilai itu benar dan sejauh mana suatu nilai itu salah. Logika fuzzy adalah suatu cara yang tepat untuk memetakan suatu ruang input kedalam suatu ruang output [3]. Fuzzy dinyatakan dalam derajat dari suatu keanggotaan dan derajat dari kebenaran. Oleh sebab itu sesuatu dapat dikatakan sebagian benar dan sebagian salah pada waktu yang sama. (Kusumadewi & Purnomo, 2010).

        Algoritma fuzzy memiliki ke 3 model yaitu model fuzzy Tsukamoto, Sugeno, dan Mamdani dan dari ke 3 model fuzzy ini memiliki mesin inferensi dan defuzzfikasi yang berbeda. Namun, artikel ini hanya akan membahas tentang model fuzzy Sugeno dan Tsukamoto beserta studi kasusnya. 

1. Model Sugeno

        Metode Sugeno hampir sama dengan penalaran Mamdani, hanya saja output (konsekuen) system tidak berupa himpunan fuzzy melainkan berupa konstanta atau persamaan linier. Metode ini diperkenalkan oleh Takagi-Sugeno Kang pada tahun 1985. Sistem fuzzy Sugeno memperbaiki kelemahan yang dimiliki oleh sistem fuzzy murni untuk menambah suatu perhitungan matematika sederhana sebagai bagian THEN. Pada perubahan ini, system fuzzy memiliki suatu nilai rata-rata tertimbang (Weighted Average Values) di dalam bagian aturan fuzzy IF-THEN.

        Sistem fuzzy Sugeno juga memiliki kelemahan terutama pada bagian THEN, yaitu dengan adanya perhitungan matematika sehingga tidak dapat menyediakan kerangka alami untuk erepresentasikan pengetahuan manusia dengan sebenarnya. Permasalahan kedua adalah tidak adanya kebebasan untuk menggunakan prinsip yang berbeda dalam logika fuzzy, sehingga ketidakpastian dari Seminar Nasional Aplikasi Teknologi Informasi 2005 (SNATI 2005) ISBN: 979-756-061-6 Yogyakarta, 18 Juni 2005 K-60 sistem fuzzy tidak dapat direpresentasikan secara baik dalam kerangka ini.

Ada dua model metode Sugeno yaitu model fuzzy sugeno orde nol dan model fuzzy sugeno orde satu.

1. Model Fuzzy Sugeno Orde Nol Bentuk Umum dari Model Fuzzy Orde Nol adalah sebagai berikut: IF (x1 is A1) o (x2 is A2) o ….. o (xn is An) THEN  z = k Dengan A1 adalah himpunan fuzzy ke-I sebagai anteseden dan k adalah suatu konstanta (tegas) sebagai konsekuen.
2. Model Fuzzy Sugeno Orde Satu  Bentuk Umum dari Model Fuzzy Orde Satu adalah sebagai berikut: IF (x1 is A1) o (x2 is A2) o ….. o (xn is An) THEN  z = p1.x1 + … pn.xn + q Dengan A1 adalah himpunan fuzzy ke-I sebagai anteseden dan p1 adalah suatu konstanta (tegas) ke-i dan q juga merupakan konstanta dalam konsekuen.

Studi Kasus Model Sugeno:

Sebuah perusahaan makanan kaleng akan memproduksi makanan jenis ABC. Dari data 1 bulan terakhir, PERMINTAAN TERBESAR mencapai 5000 kemasan/hari, dan PERMINTAAN TERKECIL 1000 kemasan/hari. PERSEDIAAN TERBANYAK digudang sampai 600 kemasan/hari, dan PERSEDIAAN TERKECIL mencapai 100 kemasan/hari. Dengan segala keterbatasan kemampuan PRODUKSI TERBANYAK adalah 7000 kemasan/hari, dan agar efisien PRODUKSI TERKECIL adalah 2000 kemasan/hari. Dalam produksi perusahaan menggunakan aturan :

R1 : JIKA permintaan TURUN dan persediaan BANYAK maka produksi = permintaan – persediaan

R2 : JIKA permintaan TURUN dan persediaan SEDIKIT maka produksi = permintaan

R3 : JIKA permintaan NAIK dan persediaan BANYAK maka produksi = permintaan

R4 : JIKA permintaan NAIK dan persediaan SEDIKIT maka produksi = 1,25 * Permintaan – Persediaan

Berapa harus diproduki jika PERMINTAAN 4000 kemasan dan PERSEDIAAN 300 kemasan?

Jawab :

Terdapat 3 variabel fuzzy yaitu (1) permintaan, (2) persediaan, dan (3) produksi

• PERMINTAAN. Terdiri dari 2 himpunan fuzzy, yaitu (1) TURUN, dan (2) NAIK. Diketahui : Permintaan terendah adalah 1000 kemasan/hari  Permintaan tertinggi adalah 5000 kemasan/hari  Permintaan permasalahan = 4000 kemasan.
•  PERSEDIAAN. Terdiri dari 2 himpunan fuzzy, yaitu (1) SEDIKIT, dan (2) BANYAK. Diketahui :  Persediaan terendah adalah 100 kemasan/hari  Persediaan tertinggi adalah 600 kemasan/hari Persediaan permasalahan = 300 kemasan.

Nilai Produksi Z

• Permintaan X

• Permintaan Y

Mencari Produksi Z

• R1 : JIKA permintaan TURUN dan persediaan BANYAK maka produksi = Permintaan – Persediaan

• R2 : JIKA permintaan TURUN dan persediaan SEDIKIT maka produksi =    Permintaan

• R3 : JIKA permintaan NAIK dan persediaan BANYAK maka produksi = Permintaan

• R4 : JIKA permintaan NAIK dan persediaan SEDIKIT maka produksi = 1,24 * Permintaan – Persediaan

Hitung z sebagai berikut:

Maka, barang yang harus diproduksi jika permintaan 4000 kemasan dan persediaan 300 kemasan adalah 4230.

2. Model Tsukamto

        Metode Tsukamoto Pada metody fuzzy Tsukamoto, proses inferensi dilakukan dengan aturan (rule) berbentuk IF-THEN dan menggunakan operasi AND, dimana akan dipilih nilai yang lebih minimum (MIN) dari dua variable yang ada.

        Menurut Kusumadewi (2010), metode Tsukamoto merupakan perluasan dari penalaran monoton. Pada metode Tsukamoto, setiap konsekuen pada aturan yang berbentuk IF-Then harus dipresentasikan dengan suatu himpunan fuzzy dengan fungsi keanggotaan yang monoton. Sebagai hasilnya, output hasil inferensi dari tiap-tiap aturan diberikan secara tegas (crisp) berdasarkan α-predikat (fire strength). Hasil akhirnya diperoleh dengan menggunakan rata-rata terbobot.

        Menurut Sutojo (2011:233) secara umum bentuk model fuzzy Tsukamoto adalah:

If (X IS A) and (Y IS B) Then (Z IS C)

Di mana A, B, dan C adalah himpunan fuzzy.

Misalkan diketahui 2 rule berikut :

IF (x is A1) AND (y is B1) Then (z is C1)

IF (x is A2) AND (y is B2) Then (z is C2)

Dalam inferensinya, metode Tsukamoto menggunakan tahapan berikut.

1. Fuzzyfikasi
2. Pembentukan basis pengetahuan Fuzzy (rule dalam bentuk IF … THEN)
3. Mesin Inferensi, menggunakan fungsi implikasi MIN untuk mendapatkan nilai α predikat tiap-tiap rule (α1, α1, α1,…. αn).
4. Defuzzyfikasi, menggunakan metode rata-rata (Average).

Studi Kasus Model Tsukamto:

Penelitian ini dilakukan di BMKG Kelas III Tanjungpinang, fokus penelitian ini adalah penerapan logika fuzzy metode Tsukamoto untuk prediksi cuaca. Data yang dibutuhkan dalam penelitian ini adalah data suhu udara, kelembaban udara, kecepatan angin, tekanan udara dan intensitas penyinaran matahari dalam bentuk harian dari tahun 2013 sampai dengan 2015 yang diperoleh dari BMKG (Badan Meteorologi Klimatogi dan Geofisika) kelas III Tanjungpinang. Sedangkan metode prediksi yang digunakan dalam penelitian ini adalah metode fuzzy Tsukamoto. Pada metode Tsukamoto implikasi setiap aturan berbentuk Sebab-Akibat atau Implikasi Input-Output dimana antara anteseden dan konsekuen harus ada hubungannya. Metode Tsukamoto menerapkan penalaran monoton pada setiap aturanya. Karena menerapkan penalaran monoton maka setiap aturan yang berbentuk IF – Then harus direpresentasikan dengan suatu himpunan fuzzy dengan fungsi keanggotaan yang monoton. Hasil dari setiap aturan inferensi akan diberikan secara tegas berdasarkan predikat. Sehingga diperoleh hasil akhir dengan menggunakan defuzzy konsep rata – rata terbobot.

Jawab :

Proses Mencari Nilai Z

Langkah-langkah untuk prediksi cuaca menggunakan metode Tsukamoto dalam penelitian ini adalah sebagai berikut:

1. Membagi data menjadi 2 kelompok, yaitu data Training dan data Test
2. Menentukan nilai domain himpunan fuzzy
3. Membuat fungsi keanggotaan masing-masing variabel
4. Pembentukan Rule aturan fuzzy
5. Pembobotan
6. Mencari nilai Alph
7. Mencari nilai 
8. Membandingkan hasil prediksi

        Data yang digunakan dalam penelitian ini adalah data rata-rata cuaca harian dalam waktu 3 tahun, di mulai dari Januari 2013 sampai dengan April 2015, data tersebut di bagi menjadi 2 yaitu data Training dan data Test. Data Training di gunakan untuk proses pelatihan dengan tujan untuk mendapatkan nilai dari domain himpunan fuzzy, fungsi keanggotaan serta untuk mendapatkan Rule. Data rata-rata cuaca pada data Training ditunjukkan pada tabel 1 berikut :

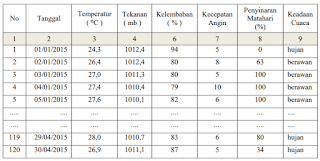
Data Test digunakan untuk pengujian dari hasil prediksi metode Tsukamoto dengan data real dari BMKG, data Test ditunjukkan pada tabel II berikut :

Setelah di dapatkannya Rule selanjutnya memasukan nilai bobot dari masing-masing variable kedalam Rule dengan tujuan untuk mendapatkan nilai Z. Variabel yang digunakan pada penelitian ini yaitu suhu udara, kelembaban udara, kecepatan angin, tekanan udara dan intensitas penyinaran matahari. Banyaknya data yang digunakan untuk penelitian ini adalah 850 dimana sebanyak 730 data digunakan untuk pelatihan dan 120 data yang digunakan untuk pengujian.

Hasil pengujian sebanyak 120 data menghasilkan total sebanyak 83 data tepat prediksi dengan hasil persentase keakuran sebesar 69,17 %. Hasil prediksi cuaca dapat dilihat pada tabel III berikut :